Evaluating and using the adjustment weights
After weights are fitted in order to balance the sample, the results should be evaluated so to understand the quality of the weighting.
Summary statistics
Summary
Printing the adjusted object gives a high level overview of the content of the object:
print(adjusted)
Output:
Adjusted balance Sample object with target set using ipw
1000 observations x 3 variables: gender,age_group,income
id_column: id, weight_column: weight,
outcome_columns: happiness
target:
balance Sample object
10000 observations x 3 variables: gender,age_group,income
id_column: id, weight_column: weight,
outcome_columns: None
3 common variables: income,age_group,gender
To generate a summary of the data, use the summary method:
print(adjusted.summary())
This will return several results:
- Covariate mean ASMD improvement: ASMD is "Absolute Standardized Mean Difference". For continuous variables, this measure is the same as taking the absolute value of Cohen's d statistic (also related to SSMD), when using the (weighted) standard deviation of the target population. For categorical variables it uses one-hot encoding.
- Design effect
- Covariate mean Adjusted Standardized Mean Deviation (ASMD) versus Unadjusted covariate mean ASMD
- Model proportion deviance explained (if inverese propensity weighting method was used)
Output:
Covar ASMD reduction: 62.3%, design effect: 2.249
Covar ASMD (7 variables): 0.335 -> 0.126
Model performance: Model proportion deviance explained: 0.174
Note that although we had 3 variables in our original data (age_group, gender, income), the asmd counts each level of the categorical variables as separate variable, and thus it considered 7 variables for the covar ASMD improvement.
Covariate Balance
We can check the mean of each variable before and after applying the weights using .mean():
adjusted.covars().mean().T
To get:
source self target unadjusted
_is_na_gender[T.True] 0.103449 0.089800 0.08800
age_group[T.25-34] 0.279072 0.297400 0.30900
age_group[T.35-44] 0.290137 0.299200 0.17200
age_group[T.45+] 0.150714 0.206300 0.04600
gender[Female] 0.410664 0.455100 0.26800
gender[Male] 0.485887 0.455100 0.64400
gender[_NA] 0.103449 0.089800 0.08800
income 9.519935 12.737608 5.99102
The self is the adjusted ASMD, while unadjusted is the unadjusted ASMD.
And .asmd() to get ASMD:
adjusted.covars().asmd().T
To get:
source self unadjusted unadjusted - self
age_group[T.25-34] 0.040094 0.025375 -0.014719
age_group[T.35-44] 0.019792 0.277771 0.257980
age_group[T.45+] 0.137361 0.396127 0.258765
gender[Female] 0.089228 0.375699 0.286472
gender[Male] 0.061820 0.379314 0.317494
gender[_NA] 0.047739 0.006296 -0.041444
income 0.246918 0.517721 0.270802
mean(asmd) 0.126310 0.334860 0.208551
We can see that on average the ASMD improved from 0.33 to 0.12 thanks to the weights. We got improvements in income, gender, and age_group.
Although we can see that age_group[T.25-34] didn't get improved.
Understanding the model
For a summary of the diagnostics measures, use:
adjusted.diagnostics()
This will give a long table that can be filterred to focus on various diagnostics metrics. For example, when the .adjust() method is run with model="ipw" (the default method), then the rows from the diagnostics output with metric == "model_coef" represent the coefficients of the variables in the model. These can be used to understand the model that was fitted (after transformations and regularization).
Visualization post adjustments
We can create all (interactive) plots using:
adjusted.covars().plot()
And get:

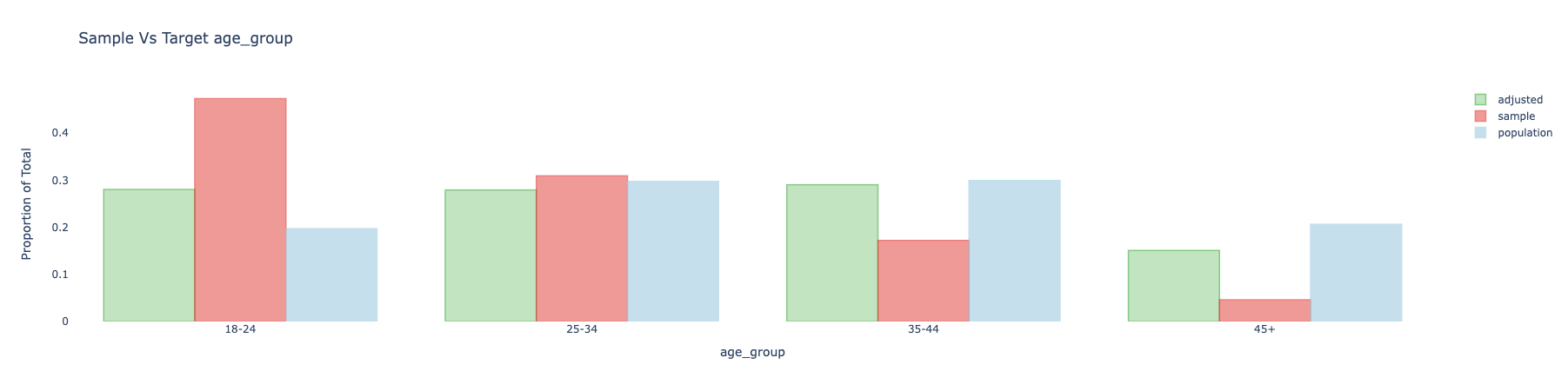
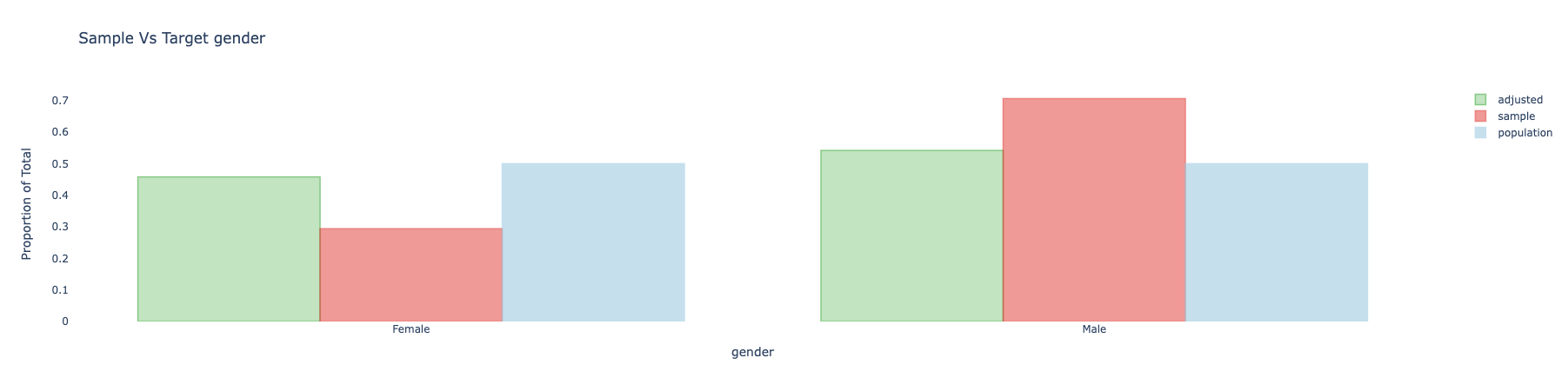
We can also use different plots, using the seaborn library, for example with the "kde" dist_type.
adjusted.covars().plot(library = "seaborn", dist_type = "kde")
And get:
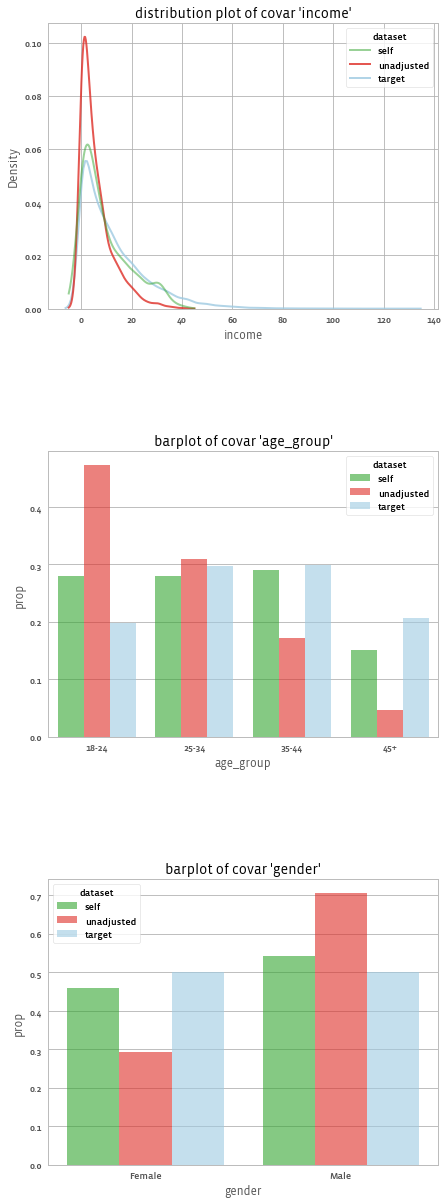
Distribution of Weights
We can look at the distribution of weights using the following method call:
adjusted.weights().plot()
And get:
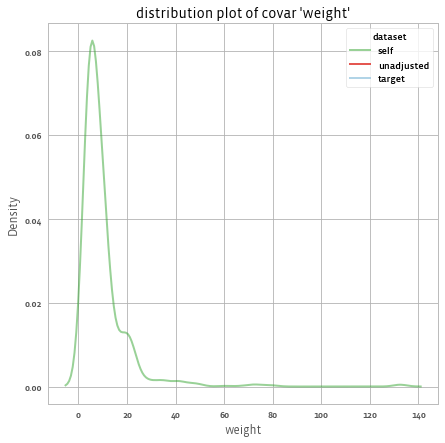
Or calculate the design effect using:
adjusted.weights().design_effect()
# 2.24937
Analyzing the outcome
The .summary() method gives us the response rates (if we have missing values in the outcome), and the weighted means before and after applying the weights:
print(adjust.outcomes().summary())
To get:
1 outcomes: ['happiness']
Mean outcomes:
happiness
source
self 54.221388
unadjusted 48.392784
Response rates (relative to number of respondents in sample):
happiness
n 1000.0
% 100.0
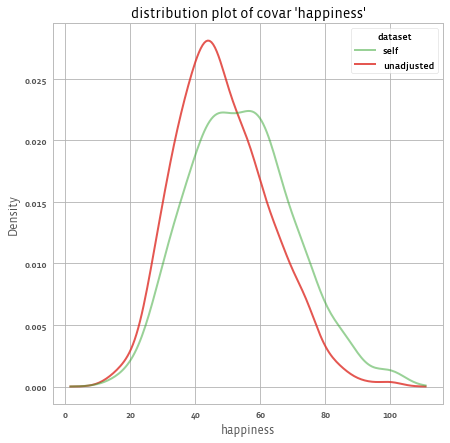
For example, we see that the estimated mean happiness according to our sample is 48 without any adjustment and 54 with adjustment. The following shows the distribution of happinnes before and after applying the weights:
adjusted.outcomes().plot()
And we get: